Définitions
1.) Population étudiée :
Groupe d’apprentis, employés d’une entreprise, habitants d’une ville, élèves d’une classe…
2.) Caractère étudié :
Ages, tailles, consommation d’eau, moyens de locomotion, nombre de frères et sœurs, lieu de repas du midi, couleur des yeux…
3.) Nature du caractère étudié :
Quantitatif : c’est un nombre
Âges, tailles, consommation d’eau, nombre de frères et sœurs…
Qualitatif : c’est un mot
Moyen de locomotion, lieu de repas, couleur des yeux…
4.) Tableau des données :
| Caractère étudié (xi) | Effectif (ni) | Fréquence (en %) (à 0,1 près) |
| …………………………………………….. | …………………………………………….. | (ni x 100) / N (produit en croix) |
| …………………………………………….. | …………………………………………….. | …………………………………………….. |
| …………………………………………….. | …………………………………………….. | …………………………………………….. |
| Total | Effectif total N = | 100 |
5.) Représentations graphiques des données :
Diagramme circulaire
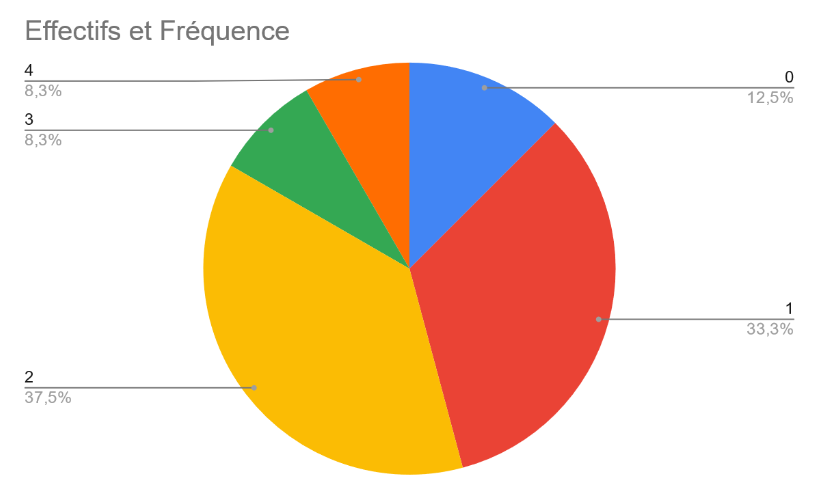
Diagramme en bâtons
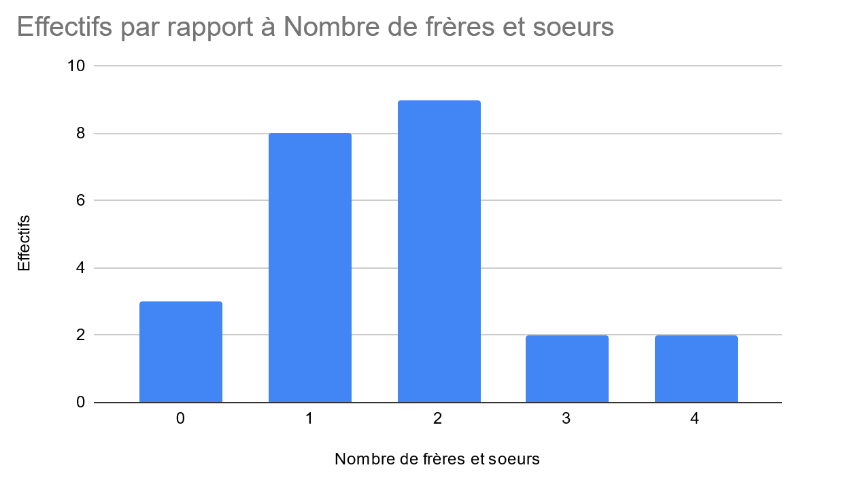
6.) Calcul de la moyenne :
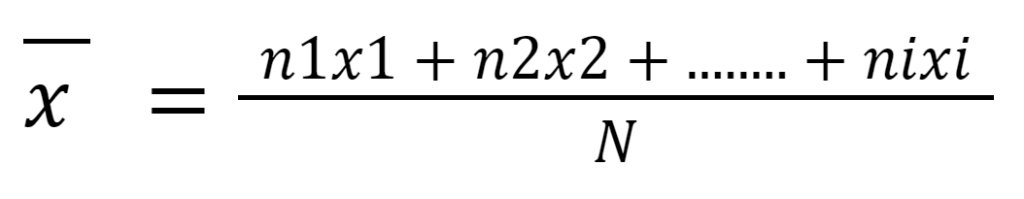
Exemple statistique sur une classe d’élèves
Nous étudions le nombre de frères et sœurs qu’ont les élèves de la classe.
Nous relevons dans le tableau ci-dessous le nombre de frères et sœurs de chaque élève.
| Population étudiée : | ………………………………………………………………………… |
| Caractère étudié : | ………………………………………………………………………… |
| Nature du caractère étudié : | ………………………………………………………………………… |
| Effectif total N : | ………………………………………………………………………… |
| Nombre total de frères et sœurs : | ………………………………………………………………………… |
| Nombre moyen de frères et soeurs (arrondi à 0,01) : | ………………………………………………………………………… |
Classer par ordre croissant la liste des réponses :
Compléter le tableau suivant :
| Nombre de frères et sœurs | Effectif | Fréquence (en %) (à 0,1 près) | Angle (°) |
| ………….. | ………….. | ………….. | ………….. |
| ………….. | ………….. | ………….. | ………….. |
| ………….. | ………….. | ………….. | ………….. |
| ………….. | ………….. | ………….. | ………….. |
| ………….. | ………….. | ………….. | ………….. |
| ………….. | ………….. | ………….. | ………….. |
| Total | N = | 100 | 360 |
Diagramme circulaire :
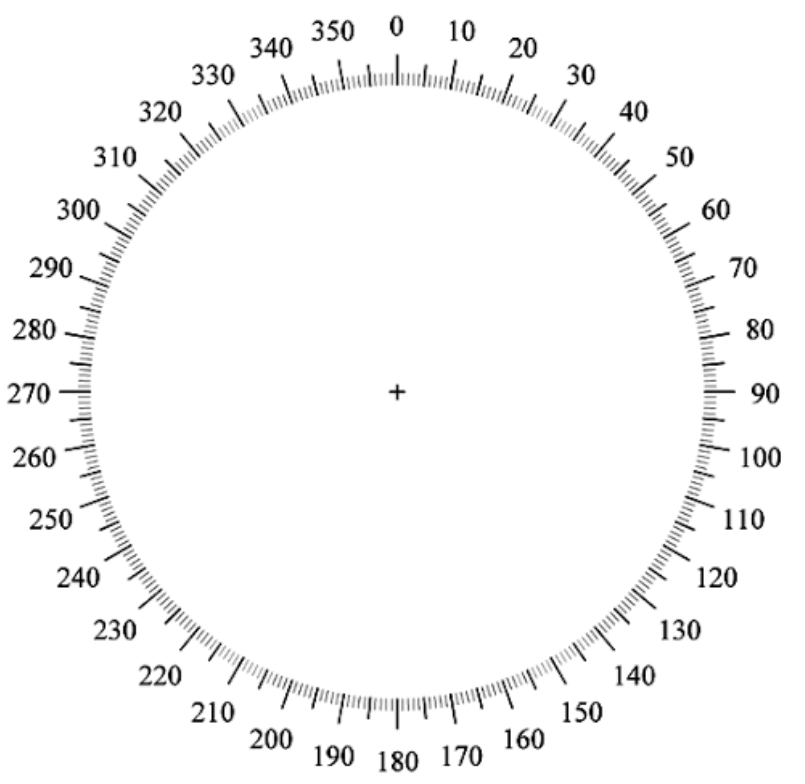
Diagramme en bâtons :
Exercices statistique
Exercice 1 : le centre de vacances
Le directeur d’un centre de vacances étudie l’âge des jeunes qui fréquentent son établissement.
Les résultats sont présentés dans le diagramme ci-contre.
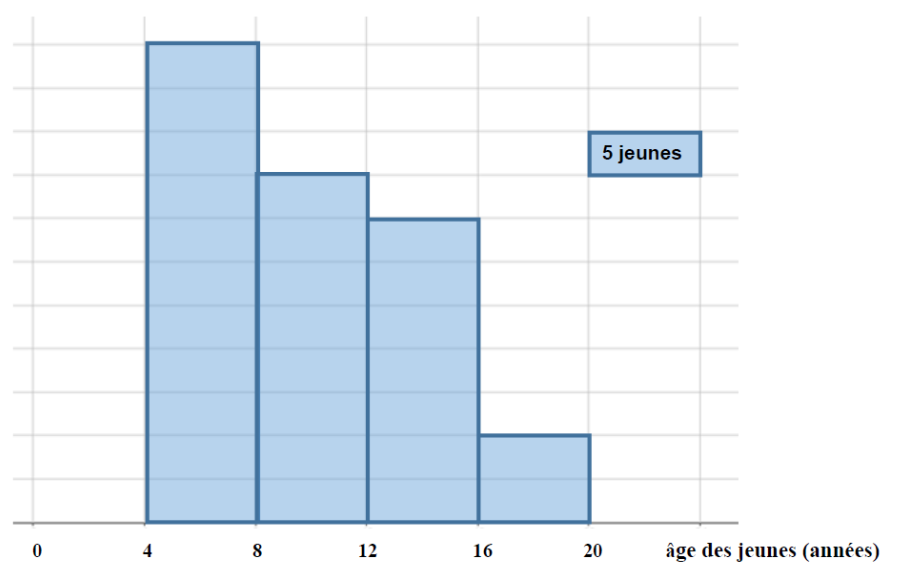
1.) Indiquer, à l’aide de l’histogramme, le nombre de jeunes qui ont entre 16 et 20 ans.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
2.) Quelle est la classe d’âges la plus représentée ? Cocher la bonne réponse.
◻ [4 ; 8[
◻ [8 ; 12[
◻ [12 ; 16[
◻ [16 ; 20[
3.) Compléter le tableau suivant :
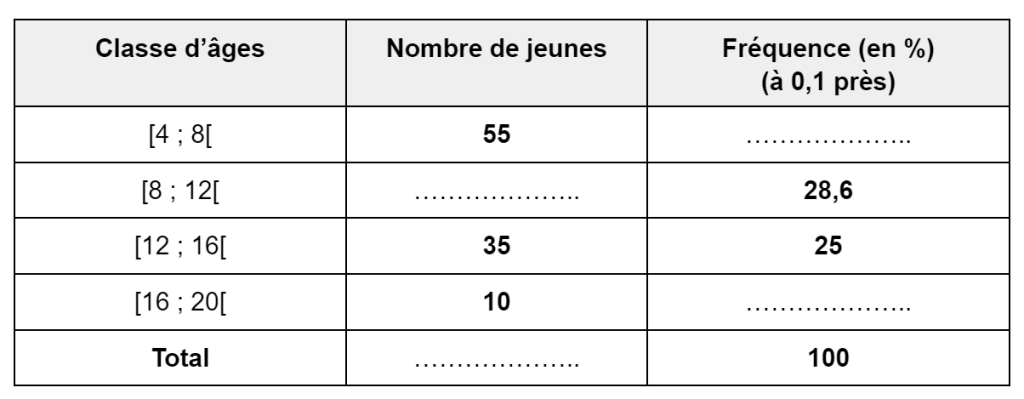
4.) Des travaux d’aménagements de l’aire de jeux doivent avoir lieu si au moins 65 % des jeunes ont moins de 12 ans. Des travaux doivent-ils être réalisés ? Justifier la réponse.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
Exercice 2 : stand à la fête foraine
Un professeur questionne le gérant d’un stand sur son bilan des repas vendus sur la première semaine d’installation à la fête foraine. En réponse, celui-ci présente à la classe les deux documents suivants :
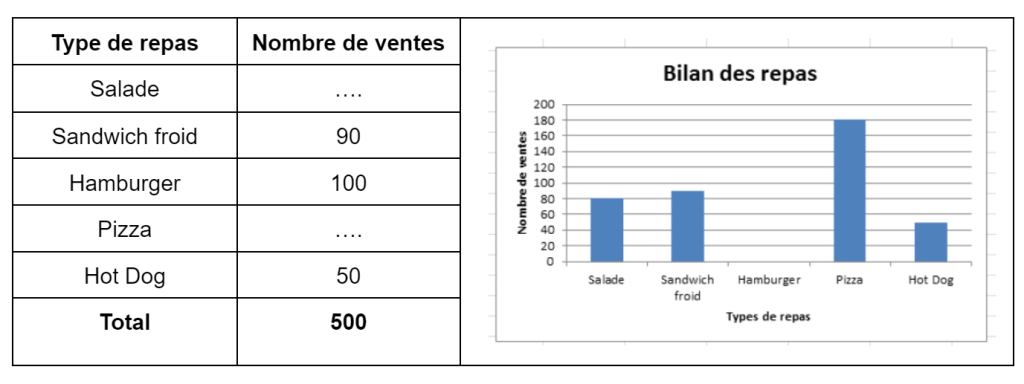
1.) Parmi les trois propositions suivantes, cocher celle qui correspond à la représentation graphique ci-dessus :
◻ diagramme en bâtons
◻ histogramme
◻ diagramme circulaire
2.) Compléter les valeurs manquantes du tableau en utilisant la représentation graphique.
3.) Compléter la représentation graphique.
4.) Indiquer le caractère étudié.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
5.) Indiquer la nature du caractère étudié.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
Le gérant soumet ensuite des documents permettant de travailler sur la rentabilité du stand, et de comparer les recettes des repas de midi et des repas du soir.
Mathieu entre dans sa calculatrice toutes les sommes encaissées et obtient grâce au mode « statistiques » les résultats suivants :
6.) À l’aide des captures d’écran reproduites ci-dessus.
Indiquer le nombre de repas servis :
le midi : ………………………………….…
le soir : …………………………….……….
7.) Indiquer la moyenne des sommes encaissées en journée et le soir :
le midi : ……..…………….………..……..
le soir : …………….…….………..……….
Exercice 3 : diagnostic de performances énergétiques
Madame Léonard a acheté un local pour ouvrir une entreprise.
Lors de l’achat du local, elle a reçu un diagnostic performance énergétique. Sa consommation énergétique estimée est 230 kWh/m² par an. Elle souhaite comparer les résultats avec des locaux voisins.
Voici les mesures énergétiques réalisées dans 10 locaux voisins du local de Madame Léonard :
Problématique : le vendeur du local déclare plus de « 80 % des 10 locaux voisins ont une consommation supérieure ou égale à 230 kWh/m² par an ». Le but de cet exercice est de vérifier si ce vendeur a raison.
1.) À l’aide du document 2, indiquer la lettre qui correspond à la consommation énergétique du local de madame Léonard.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
2.) Déterminer les valeurs des consommations minimale et maximale parmi les 10 locaux voisins.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
3.) Indiquer le caractère étudié aux questions précédentes. Préciser s’il est qualitatif ou quantitatif.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
4.) Cocher la méthode la plus adaptée pour répondre à la problématique.
◻ une résolution graphique à l’aide d’une fonction.
◻ une étude statistique en calculant des fréquences.
◻ une mise en équation.
5.) Une partie des mesures énergétiques des dix locaux ont été rassemblées dans un tableur.
Compléter les cellules B2 et B5.
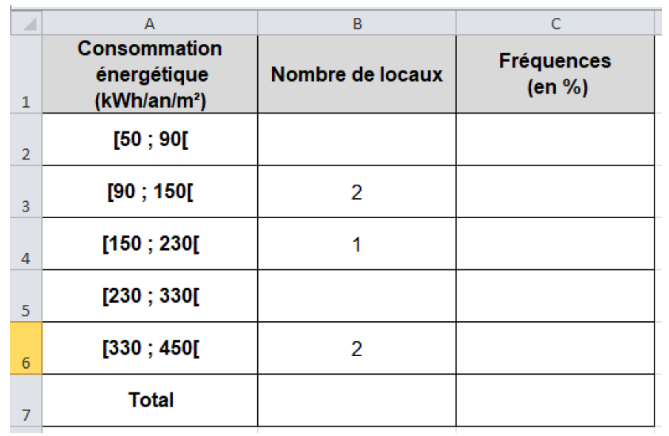
6.) Vérifier que l’effectif total vaut N = 10 (détailler le calcul). Placer cette valeur dans le tableau précédent.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
7.) On s’intéresse aux locaux dont la consommation est comprise dans l’intervalle [150 ; 230[. Calculer, en pourcentage, la fréquence correspondante.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
8.) Cocher la formule qu’il faut saisir dans la cellule C4 pour obtenir le résultat de la question 7.)
◻ = (B4/B7)*100
◻ = moyenne(B2:B6)
◻ = B4+B7
◻ = somme(B2:B6)
9.) Compléter le tableau avec les valeurs manquantes.
10.) Calculer le pourcentage de locaux dont la consommation énergétique est supérieure ou égale à celle de Madame Léonard.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
11.) Répondre à la problématique. Justifier la réponse.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
Compétences, capacités et connaissances issues du programme CAP Mathématiques Education Nationale
Capacités
Recueillir et organiser des données.
Calculer un effectif total, calculer des fréquences, mentalement dans quelques cas simples*, avec une calculatrice ou un tableur dans les autres cas.
Lire et interpréter les données d’une série statistique présentées dans un tableau ou représentées graphiquement, sous forme de classes ou non.
Représenter une série statistique par un diagramme en bâtons ou circulaire, sur papier dans quelques cas simples puis à l’aide d’un logiciel.
Calculer la moyenne d’une série statistique mentalement dans quelques cas simples*, avec une calculatrice ou un tableur dans les autres cas.
Connaissances
Regroupement par classes d’une série statistique.
Effectifs, fréquences.
Diagrammes en bâtons, diagrammes circulaires.
Moyenne.