Définition
Résoudre une équation c’est une quête. C’est partir à la recherche d’un nombre inconnu !
Pour nous guider dans notre quête et nous aider à connaître ce nombre, une histoire nous est racontée.
1.) La quête :
Quel est, en cm, le record de saut en hauteur ?
2.) L‘histoire :
Si tu multiplies par 30 ce record et que tu lui retires 1301 tu obtiendras le nombre réponse du rébus ci-dessous.
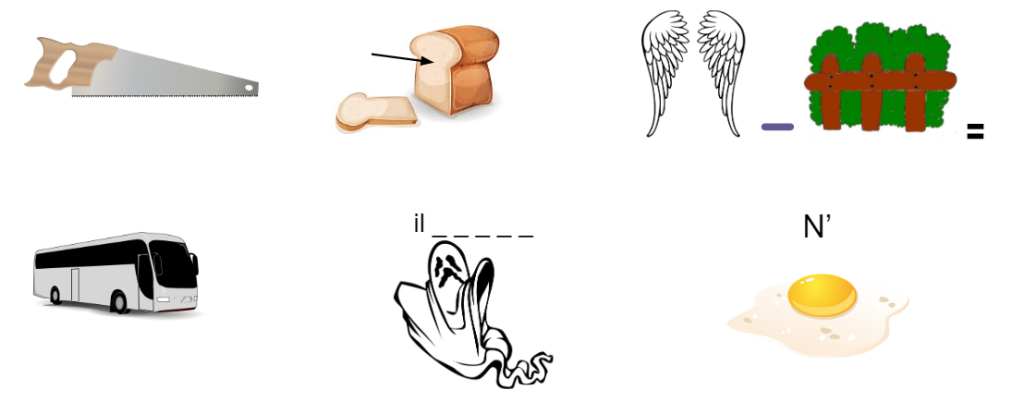
Réponse du rébus : …………………………………………………………….
Proposition de solution :
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
Résoudre une équation
C’est chercher à isoler l’inconnue x pour trouver sa valeur! Et pour cela il faut respecter quelques règles.
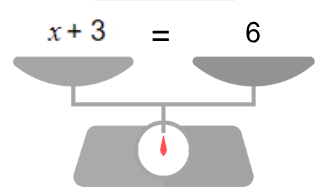 | x + 3 = 6 x + 3 – 3 = 6 – 3 x = 6 – 3 x = 3 |  Le plus devient moins |
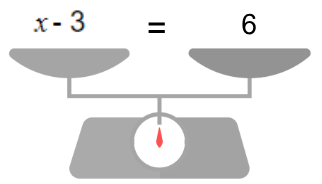 | x – 3 = 6 x – 3 + 3 = 6 + 3 x = 6 + 3 x = 9 | 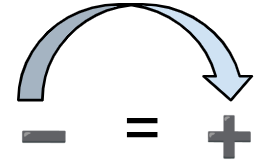 Le moins devient plus |
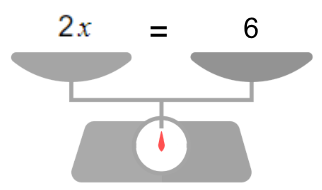 | 2x = 6 2x/2 = 6/2 x = 6/2 x= 3 | 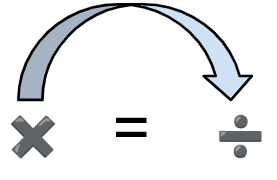 Le multiplier devient diviser |
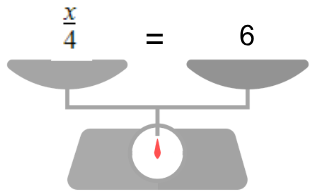 | x/4 = 6 (x/4) * 4 = 6 * 4 x= 6 * 4 x = 24 |  Le diviser devient multiplier |
Etapes de résolution d’une équation
1.) Déterminer l’inconnue :
Soit x la hauteur du record, en cm
2.) Traduire l’histoire en langage mathématique : l’équation
………………………… 〓 …………………………….
3.) Appliquer, ligne par ligne, les règles de résolution d’équation pour découvrir x
| Les règles | La résolution |
| ………………………… 〓 …………………… | |
| ………………………… 〓 ……………………. | |
| ………………………… 〓 ……………………. | |
| ………………………… 〓 ……………………. | |
| x 〓 ……………………. |
Exercice équations
Exercice 1 : devine le nombre niveau 1
Compléter ( dans chaque équation “…..” désigne le même nombre inconnu ).
3 + ….. = 6
9 + ….. = -3
8 – ….. = -3
6 – ….. = 2
27 = 3 + …..
8 – ….. = 3 + ….. + 1
6 + ….. = 54
-15 – ….. = 11
150 + ….. = 180 – …..
Exercice 2 : devine le nombre niveau 2
2 x ….. = 6
…… / 7= 8 x ….. – 165
…… / 6 = 8
….. x 7 = 42
2 x ….. = 4 x ….. – 12
…… / 3 – 4 = 8
Exercice 3 : résoudre les équations
3x = 12
……………………….
……………………….
3x + 23 = 62
……………………….
……………………….
– 12x + 56 = 88
……………………….
……………………….
(3x + 5) – (2x – 4) = 61
……………………….
……………………….
x + 6 = -5
……………………….
……………………….
6x – 150 = 7x
……………………….
……………………….
100x + 10 = 600x+1010
……………………….
……………………….
4 – (5 – 2x) = 4x+2(7x – 1)
……………………….
……………………….
Exercice 4 : respecter le budget.
Pour la réalisation d’une plaquette présentant l’ensemble des salades, sandwichs et autres paninis au choix du client, un restaurateur contacte une société d’infographie qui lui propose le tarif suivant : 174,95 € de frais pour la conception de la plaquette auquel on ajoute 0,25 € par exemplaire.
Le restaurateur ne peut pas dépasser 300 euros pour ce budget.
- Calculer le coût de revient pour un tirage de 500 exemplaires.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
- Calculer le coût de revient pour un tirage de 501 exemplaires.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
- Déterminer le nombre d’exemplaires qu’il peut obtenir pour un budget maximum de 300 euros. Justifier.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
- Soit x le nombre de plaquettes pour lequel le coût est de 300 €. Ecrire l’équation correspondante :
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
- Résoudre cette équation.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
- Est-ce que le résultat de l’équation confirme la réponse 3) ? Justifier.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
Exercice 5 : devine mon salaire.
Je dépense le quart de mon salaire pour me loger, les 3/7 pour me nourrir. Il me reste 594 € pour les autres dépenses. Quel est mon salaire ?
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
Exercice 6 : devine les deux nombres.
Trouve deux naturels pairs consécutifs dont la somme est 206 ?
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
Exercice 7 : devine les trois nombres.
Trouver trois nombres consécutifs dont la somme est égale à 378.
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
Exercice 8 : devine les frais de livraison.
Le montant d’une facture s’élève à 480 €. Il comprend le prix d’achat des marchandises augmenté des frais de transport s’élevant à 5% du prix d’achat. Quel est le montant des frais de transport ? ( on désignera par x le prix d’achat des marchandises )
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
Exercice 9 : combien de temps pour mettre 45 km dans la vue.
Deux voitures partent au même instant d’un poste de péage situé sur l’autoroute et roulent dans le même sens, l’une à la vitesse de 100 km/h, l’autre à la vitesse de 130 km/h. Au bout de combien de temps seront-elles distantes de 45 km ?
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
Compétences, capacités et connaissances issues du programme CAP Mathématiques Education Nationale
Résolution d’un problème du premier degré
Capacités
Résoudre algébriquement une équation du type ax + b = c*, où x est l’inconnue (a, b et c étant des nombres réels, et a non nul).
Modéliser un problème par une équation du premier degré à une inconnue et le résoudre.
Connaissances
Méthode de résolution algébrique d’une équation du premier degré à une inconnue.

