La clarté des raisonnements et la qualité de la rédaction interviendront pour une part importante dans l’appréciation des copies.
Les candidats répondent directement sur le sujet.
L’usage de la calculatrice avec mode examen actif est autorisé.
L’usage de la calculatrice sans mémoire, « type collège », est autorisé.
Dans la suite du document, ce symbole signifie « Appeler l’examinateur ».
★ = 1 pt ☆ = 0,5 pt
Freinage sur route mouillée, distance d’arrêt et obstacle

Vous êtes en train de conduire. Il pleut. Un obstacle arrive sur la route à 100 mètres devant vous.
Vous freinez. La voiture parcourt une certaine distance pour s’arrêter : c’est la distance d’arrêt, notée dA.
Cette distance d’arrêt dA se compose de :
– la distance dR parcourue par le véhicule pendant le temps de réaction.
– la distance dF parcourue par le véhicule pendant le freinage.
dA = dR + dF
En fonction de sa vitesse, le véhicule heurtera ou non l’obstacle.

Problématique : Quelle est la vitesse à ne pas dépasser pour pouvoir s’arrêter avant l’obstacle ?
Partie 1 : Estimation de la distance d’arrêt

1.) Estimer d’après le document 1, un encadrement de la vitesse v à ne pas dépasser pour éviter l’obstacle :
Sur route sèche on peut estimer que la vitesse v doit être comprise entre ……..km/h et …….. km/h
Sur route humide on peut estimer que la vitesse v doit être comprise entre ……..km/h et …….. km/h
☆ C1

Présenter et expliquer oralement votre estimation
☆☆ C5
Partie 2 : distance de freinage
La distance de freinage peut être déterminée par la relation suivante :
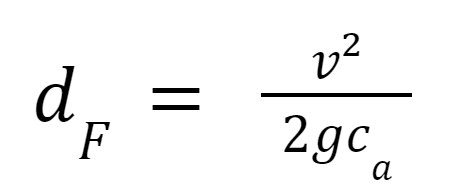
dF : distance de freinage (m)
v : vitesse (m/s)
g : intensité de la pesanteur (9.81 m/s²)
ca : coefficient d’adhérence
On considérera un coefficient d’adhérence (ca) sur route sèche à 0,7 et un coefficient d’adhérence sur route mouillée à 0,4.
2.) Calculer, en m, la distance de freinage à 72 km/h (20 m/s) sur route sèche, arrondir à l’unité :
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆ C3
3.) Calculer, en m, la distance de freinage à 72 km/h sur route mouillée, arrondir à l’unité :
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆ C3
Le graphique ci-dessous représente l’évolution de la distance de freinage (en m) en fonction de la vitesse (en m/s) sur route sèche et sur route mouillée.
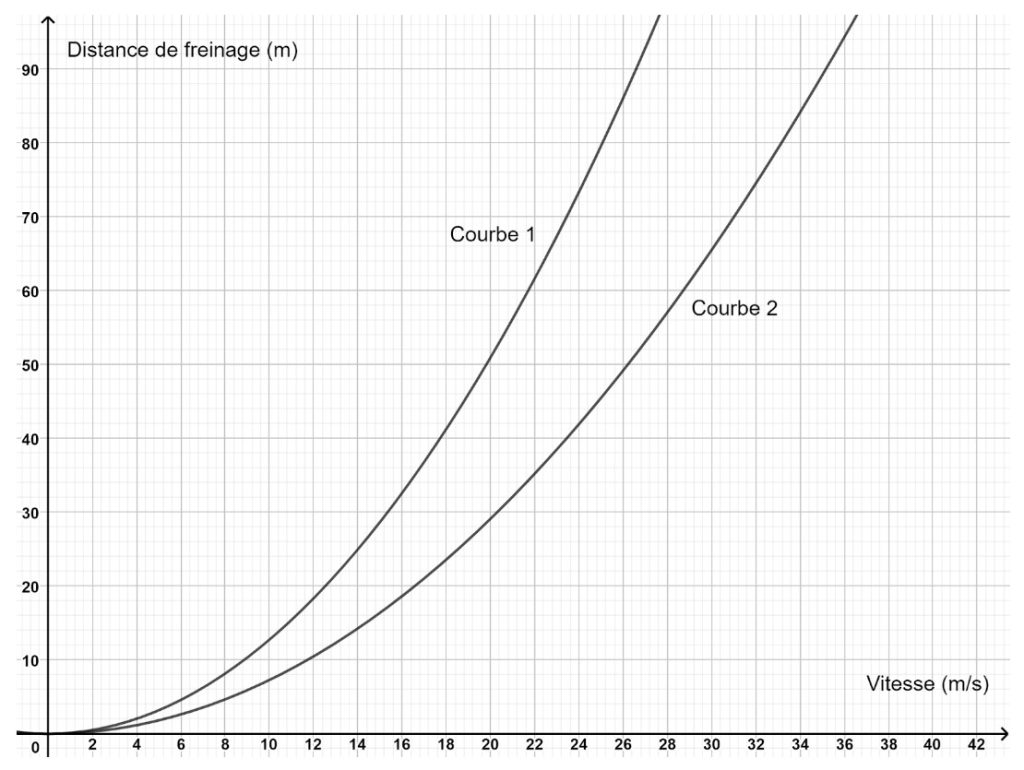
4.) La courbe 1 représente l’évolution de la distance de freinage (en m) en fonction de la vitesse (en m/s) :
◻ Sur route sèche
◻ Sur route humide
☆ C2
5.) La courbe 2 représente l’évolution de la distance de freinage (en m) en fonction de la vitesse (en m/s) :
◻ Sur route sèche
◻ Sur route humide
☆ C2
6.) Déterminer graphiquement la vitesse, en m/s, arrondie à l’unité, correspondant à une distance de freinage de 75 m sur route mouillée.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆ C1
Partie 3 : distance d‘arrêt
Dans la suite de l’exercice on considère une distance de freinage sur route humide telle que :
dF = 0,13v²
On considère également un temps de réaction du conducteur égal à t = 0,9 s.
La distance parcourue pendant ce temps de réaction est dR = 0,9v
7.) Exprimer, sur route humide, la distance d’arrêt dA en fonction de v :
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆ C2
Afin de répondre à la problématique, on étudie la fonction :
f(x) = 0,13x² + 0,9x sur l’intervalle [0;40] (x est la vitesse en m/s)
8.) Déterminer f’(x) où f’ est la fonction dérivée de la fonction f :
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆☆ C3
9.) Compléter le tableau de variation de la fonction f :

☆☆ C1
10.) La vitesse xmax (en m/s) à ne pas dépasser pour éviter le choc avec l’obstacle est telle que f(xmax) = 100.
Tracer la fonction f à l’aide de la calculatrice et déterminer graphiquement xmax (arrondir à l’unité) :
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆☆ C3 (TIC)

Présenter le tracé de la courbe (fenêtre bien réglée) et expliquer votre méthode pour déterminer xmax
☆☆ C5 (TIC)
11.) La vitesse x (en m/s) à ne pas dépasser pour éviter le choc avec l’obstacle est solution de l’équation du second degré suivante. Résoudre cette équation sur l’intervalle [0;40] par la méthode de votre choix :
0,13x² + 0,9x -100 = 0
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆☆ C4
12.) Répondre à la problématique en précisant la vitesse à ne pas dépasser en km/h, arrondie à l’unité :
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
☆ C5
Compétences, capacités et connaissances issues du programme BAC PRO Première Mathématiques et du programme BAC PRO Terminale Mathématiques Education Nationale
Capacités
Utiliser les formules et les règles de dérivation pour déterminer la dérivée d’une fonction polynôme de degré inférieur ou égal à 2.
Dresser le tableau de variations d’une fonction polynôme de degré inférieur ou égal à 2.
Visualiser, à partir de la représentation graphique d’une fonction polynôme ƒ de degré 2, le nombre possible de solution(s) de l’équation ƒ(x) = 0.
Utiliser les formules et les règles de dérivation pour déterminer la dérivée d’une fonction polynôme de degré inférieur ou égal à 3.
Dresser, à partir du signe de la dérivée, le tableau de variations d’une fonction polynôme de degré inférieur ou égal à 3.
Exploiter le tableau de variations d’une fonction polynôme ƒ de degré inférieur ou égal à 3 pour :
- déterminer le nombre des solutions de l’équation ƒ(x) = c, où c est un nombre réel ;
- déterminer les éventuels extremums locaux de la fonction ƒ.
Connaissances
Fonction dérivée d’une fonction dérivable sur un intervalle.
Notation ƒ’.
Fonctions dérivées des fonctions affines et carré.
Règles de dérivation : dérivée du produit d’une fonction dérivable par une constante, dérivée de la somme de deux fonctions dérivables.
Fonction polynôme de degré inférieur ou égal à 2.
Fonction polynôme de degré 2 à coefficients réels.
Nombre de solutions réelles de l’équation ƒ(x) = 0 où ƒ est une fonction polynôme de degré 2.
Compétence – C1
S’approprier
Rechercher, extraire et organiser l’information.
Traduire des informations, des codages.
Compétence – C2
Analyser
Raisonner
Émettre des conjectures, formuler des hypothèses.
Proposer une méthode de résolution.
Choisir un modèle ou des lois pertinentes.
Élaborer un algorithme.
Choisir, élaborer un protocole.
Évaluer des ordres de grandeur.
Compétence – C3
Réaliser
Mettre en œuvre les étapes d’une démarche.
Utiliser un modèle.
Représenter (tableau, graphique…), changer de registre.
Calculer (calcul littéral, calcul algébrique, calcul numérique exact ou approché, instrumenté ou à la main).
Mettre en œuvre un algorithme.
Expérimenter – en particulier à l’aide d’outils numériques (logiciels ou dispositifs d’acquisition de données…).
Faire une simulation.
Effectuer des procédures courantes (représentations, collectes de données, utilisation du matériel…).
Mettre en œuvre un protocole expérimental en respectant les règles de sécurité à partir d’un schéma ou d’un descriptif.
Organiser son poste de travail.
Compétence – C4
Valider
Exploiter et interpréter les résultats obtenus ou les observations effectuées afin de répondre à une problématique.
Valider ou invalider un modèle, une hypothèse en argumentant.
Contrôler la vraisemblance d’une conjecture.
Critiquer un résultat (signe, ordre de grandeur, identification des sources d’erreur), argumenter.
Conduire un raisonnement logique et suivre des règles établies pour parvenir à une conclusion (démontrer, prouver).
Compétence – C5
Communiquer
À l’écrit comme à l’oral :
rendre compte d’un résultat en utilisant un vocabulaire adapté et choisir des modes de représentation appropriés ;
expliquer une démarche.

